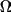In the stochastic framework the reaction and diffusion events are treated probabilistically and the state changes in discrete steps when an event occurs. The probability that a certain reaction, , occurs in a subvolume with volume during the next time 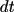is modelled as 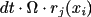, where it is indicated that the rate 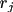depends on the concentrations of reactants 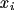in subvolum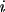e . The expressions are given in the SBML model description and they should evaluate in concentration per time. For instance the rate law of the reaction 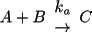can be defined as 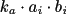in the SBML file. Here and are given in molar and the second order rate constant of association 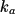is given in per molar per second 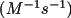. MesoRD interprets the rate as a probability per time unit by evaluating the expression , where 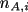and 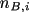are number of A and B molecules in the subvolume, 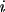. If this reaction occurs the number of A and B molecules in the subvolume are reduced by one and the number of C molecules is increased by one. Generally the number of molecules will change by the stoichiometry defined for the reaction in the SBML file.

The event that a molecule diffuses to a neighbouring subvolume is treated as a first order reaction with a rate constant of 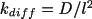, where is the diffusion constant for the diffusing species and 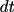is the side length of the subvolume. The probability that an A molecule diffuses from one subvolume to one of its neighbours in the next short time period 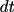is thus 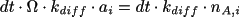, where is the concentration of A molecules in the subvolume from which the molecules diffuse. If a diffusion event occurs the number of molecules in decreased by one in the subvolume that lost a molecule and the number is increased by one in its neighbour.

The rates, i.e. the probabilities per time unit, of all different diffusion and reaction events define a stochastic process. All events are assumed to be elementary, why the time to the next event of each kind is exponentially distributed in time with a mean corresponding to the inverse of the rate. When one event occurs, some of the rates for the next event will change. In the stochastic mode, MesoRD samples the stochastic process one event at the time and updates the state and reaction rates accordingly. Since there can be millions of different events to chose from, it is critical to do this very efficiently. The algorithm used for sampling the process is the next subvolume method (NSM). The algorithm is published as supplementary material to [Elf and Ehrenberg 2004] but can also be downloaded from the MesoRD homepage.