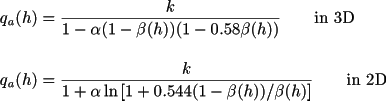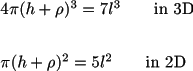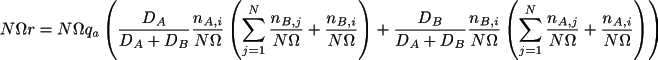When small subvolumes are needed in 3D, or when running 2D
simulations, it is often necessary to use scale dependent
association and dissociation rates constants [Fange et al. 2010]. In 2D simulations it is, in fact, a
requirement to use the scale dependent reaction rates. In 3D
simulations the scale dependent rate constant,
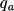 below, will converge to the macroscopic association rate
constant when the subvolumes are large and/or the reactions are
not diffusion controlled. In the latter case, the scale
dependent reaction rate constants can be turned off.
below, will converge to the macroscopic association rate
constant when the subvolumes are large and/or the reactions are
not diffusion controlled. In the latter case, the scale
dependent reaction rate constants can be turned off.
The scale dependent association rates are calculated according to
Here k is the microscopic association rate
constant on the reaction radius (see Figure 3.13, “
The XML definition of
AssociationRateConst.
”),
α is the degree of diffusion control
(see Figure 3.15, “
The XML definition of
DegreeOfDiffusionControl.
”)
and
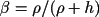 where ρ is the reaction radius (see
Figure 3.14, “
The XML definition of
where ρ is the reaction radius (see
Figure 3.14, “
The XML definition of
ReactionRadius.
”),
and h thickness of a concentric shell
centred around one of the reactants. When the other reactant is
within the shell, a reaction can occur.
Since MesoRD does not use spherical shells around molecules, rather a cartesian grid, h needs to chosen in the particular way described below. Since a molecule can reside anywhere within a subvolume, the region in which a molecule can react with its reaction partner should not only include the subvolume in which the molecule resides, but also its nearest neighbours. By requiring that the reaction volumes for the spherical case and the cartesian case should be the same, h is chosen to fulfil the relation
where l is the subvolume size.
The reaction rates must be calculated in agreement with the fact that reactions can occur within the center subvolume and its nearest neighbours [16] . In MesoRD this a achieved as follows. Using the example above where A and B react for form C, the reaction rate is calculated as
where N is the number of neighbouring
subvolumes to subvolume i, and
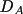 and
and
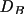 are the diffusion rates of A and B respectively. Each
combination of A and B molecules in the neighbours and center
subvolume is, however, sampled independently such that only
neighbours which actually have a molecule are selected for a
reactive event. Upon an association reaction event the product
molecule is always placed in the centre subvolume,
i. Upon a dissociation event, the two
products are distributed uniformly among the neighbours and the
centre subvolume. Here the probablity of placing reactant A in
the center subvolume is
are the diffusion rates of A and B respectively. Each
combination of A and B molecules in the neighbours and center
subvolume is, however, sampled independently such that only
neighbours which actually have a molecule are selected for a
reactive event. Upon an association reaction event the product
molecule is always placed in the centre subvolume,
i. Upon a dissociation event, the two
products are distributed uniformly among the neighbours and the
centre subvolume. Here the probablity of placing reactant A in
the center subvolume is
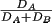 and the probability of placing reactant B in the center
subvolume is
and the probability of placing reactant B in the center
subvolume is
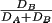 . The fractions of diffusion-rates defining the probability of
selecting a specific reactant from the center subvolume were
introduced in MesoRD version 1.1. Previous release (1.0) assumed
the same diffusion-rates for both reactants.
. The fractions of diffusion-rates defining the probability of
selecting a specific reactant from the center subvolume were
introduced in MesoRD version 1.1. Previous release (1.0) assumed
the same diffusion-rates for both reactants.
[16] Reactions can occur in neighbouring subvolumes because diffusion events includes mixing time, and diffusion limited reactions does not always have time to mix. Furthermore, in a discretised system the resolution is always twice as large as discretisation length.