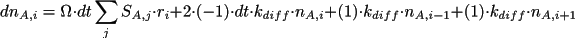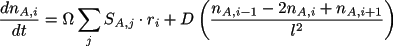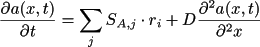In the deterministic mode MesoRD will do what we call a mean-field approximation. The approximation is that the state, i.e. number of molecules, change continuously and with the average rate given by the stochastic description at each point in time. To see what this means, consider the events that changes the number of A-molecules in subvolume 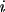during the next time period 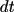, assuming that the systems has only one spatial dimension. 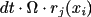The different reactions occurs with probability and when reaction occurs the number of A-molecules changes by 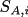. The A-molecules can also diffuse away with probability 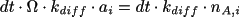to each of the two neighbouring subvolumes in one dimension. The number of A-molecules in subvolume 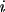can also increase if A-molecules diffuse from the neighbouring subvolumes. 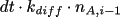They do this with probability and 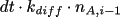, respectively. The average change in the number of A-molecules in subvolume 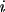during 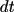is therefore

Equation 6.4. 

where the values in parenthesis are the stoichiometries for changes of the number of A-molecules of the different events. Similar expressions simultaneously govern the A-molecules in other subvolumes and other species.

If we divide Equation 6.4 by 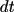we get a system of ordinary differential equations, for instance for

Equation 6.5. 

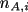
where 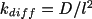. In the deterministic mode MesoRD solve this kind of ODE systems numerically.

If we divide Equation 6.5 by 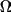and take the limit 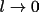we get a more familiar expression for the reactions diffusion equation

Equation 6.6. 

with as the continuous spatial coordinate.